Altitude Tracking

TOPIC:Altitude tracking

OBJECTIVE: To use geometry to find the altitude of model rockets

DESCRIPTION: In this activity, students construct simple altitude tracking devices that are used to measure the angle a rocket reaches above ground, as seen from a remote tracking site. The angle is drawn on a graph and the altitude is read from a scale.
EDITED BY: Roger Storm, NASA Lewis Research Center

Materials and Tools:

• Altitude Tracker patterns
• Thread or lightweight string
• Scrap file folders or poster board
• Glue
• Cellophane tape
• Small washer
• Scissors
• Meter stick or steel tape measure (metric)

CLICK HERE TO GET FULL SIZED TEMPLATE TO PRINT

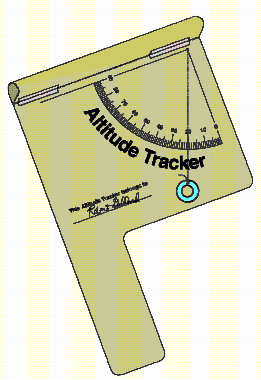
Procedure: Constructing the Altitude Tracker

1. Copy the Altitude Tracker pattern on white or colored paper. Cut out the outline and glue the pattern to a piece of scrap file folder or poster board. Do not glue the hatched area to the folder or poster board.
2. Cut off the excess file folder or poster board.
3. Roll the hatched area at the top of the pattern into a tube and tape the upper edge along the dashed line at the lower edge. Shape the paper into a sighting tube.
4. Punch a tiny hole in the apex of the protractor quadrant.
5. Cut out the Altitude Calculator and punch a hole at the apex of its protractor quadrant. Glue the Altitude Calculator to the back of the tracker so that the two holes line up.
6. Slip a thread or lightweight string through the holes. Knot the thread or string on the calculator side.
7. Hang a small washer from the other end of the thread as shown in the diagram of the completed tracker.

Procedure: Using the Altitude Tracker

1. Select a clear spot for launching water or bottle rockets.
2. Measure a tracking station location exactly 30 meters away from the launch site.
3. As a rocket is launched, the person doing the tracking will follow the flight with the sighting tube on the tracker. The tracker should be held like a pistol. Continue to aim the tracker at the highest point the rocket reached in the sky. Have a second student read the angle the thread or string makes with the quadrant protractor.

Procedure: Determining the Altitude

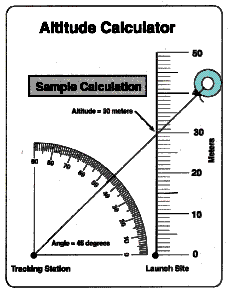
1. Use the Altitude Calculator to determine the height the rocket reached. To do so, pull the thread or string through the hole in the tracker to the Altitude Calculator side until the washer stops it. Lay the string across the protractor quadrant and stretch it so that it crosses the vertical scale. (See sample calculation.)
2. Read the altitude of the rocket. The altitude is the intersection point of the string and the vertical scale to that number. Add the height of the person holding the tracker to determine the altitude the rocket reached.

Discussion:

This activity makes use of simple trigonometry to determine the altitude a rocket reaches in flight. The basic assumption of the activity is that the rocket travels straight up from the launch site. If the rocket flies away at an angle other than 90 degrees, the accuracy of the procedure is diminished. For example, if the rocket flies toward a tracking station as it climbs upward, the altitude calculation will yield an answer higher than the actual altitude reached. On the other hand, if the rocket flies away from the station, the altitude measurement will be lower than the actual value. Tracking accuracy can be increased, however, by using more than one tracking station to measure the rocket's altitude. Position a second or third station in different directions from the first station. Average the altitude measurements.

Teaching Notes and Questions:

• This activity is simple enough so each student can construct his or her own Altitude Tracker. Permit each student to try taking measurements while other students launch the rockets. To assure accuracy in taking measurements, practice measuring the height of known objects such as a building or a flagpole. It may also be necessary for a few practice launches to familiarize each student with using the tracker in actual flight conditions.
• Why should the height of the person holding the tracker be added to the measurement of the rocket's altitude?
• Curriculum guides for model rocketry (available from model rocket supply companies) provide instructions for more sophisticated rocket tracking measurements. These activities involve two station tracking with altitude and compass direction measurement and trigonometric functions.

Additional Activities

• Construct models of historical rockets. Refer to the reference list for picture books on rockets to use as information on the appearance of various rockets. Use scrap materials for the models such as:
• Mailing tubes
• Tubes from paper rolls
• Spools
• Coffee creamer packages (small plastic containers that look like rocket engine nozzles)
• Cardboard
• Egg-shaped hosiery packages (for nose cones)
• Styrofoam cones, spheres, and cylinders
• Glue
• Tape
• Use rockets as a theme for artwork. Teach perspective and vanishing point by choosing unusual angles, such as a birds-eye view for picturing rocket launches.
• Research the reasons why so many different rockets have been used for space exploration.
• Design the next generation of spaceships.
• Compare rockets in science fiction with actual rockets.
• Follow up the rocket activities in this guide with construction and launch of commercial model rockets. Rocket kits and engines can be purchased directly from the manufacturer. Obtain additional information about model rocketry by contacting the

         
National Association of Rocketry
         P.O. Box 177
         Altoona, WI  54720.

Or try these sites:




MODEL ROCKETRY FOR EDUCATORS




ROCKETRY PAGE




ROCKETRY




3...2...1...BLASTOFF! 

BACK TO LIST OF ROCKET ACTIVITIES